自作マクロ機能のAIアップグレード：配列の貼り付け
生成系ＡＩの出現により、Excel マクロも随分と作りやすくなった。
そこで今回も、以前作成したものを改めてAIに添削してもらった。
素材となるのはこちら。
infoment.hatenablog.com
この中のうち、配列を指定範Excelでユーザー定義関数を作成。
AIへの指示がこちら。
関数名：PasteArray
引き数 target_range as range 配列を張り付ける開始点
引き数 source_array as variant 張り付けられる配列
引き数 optional transpose_flag as boolean=false 縦横を入れ替えて貼り付け戻り値
0の場合 正常終了
－1の場合 異常終了 ※target_arrayが配列ではない
－2の場合 異常終了 ※配列の次元数が3以上囲に張り付ける機能を作り直してみよう。
出来てきたのがこちら。
Function PasteArray(target_range As Range, source_array As Variant, Optional transpose_flag As Boolean = False) As Integer Dim i As Long, j As Long Dim numRows As Long, numCols As Long On Error GoTo ErrorHandler ' 配列が2次元または1次元であるかどうかを確認 If IsArray(source_array) = False Then PasteArray = -1 Exit Function End If ' 配列の次元数を取得 Select Case True Case IsArray(source_array) If Not (IsArray(source_array) And IsArray(source_array(1))) Then ' 1次元配列の場合 numRows = 1 numCols = UBound(source_array) - LBound(source_array) + 1 Else ' 2次元配列の場合 numRows = UBound(source_array, 1) - LBound(source_array, 1) + 1 numCols = UBound(source_array, 2) - LBound(source_array, 2) + 1 End If Case Else PasteArray = -2 Exit Function End Select ' 縦横を入れ替える場合 If transpose_flag Then For i = 1 To numCols For j = 1 To numRows target_range.Cells(i, j).Value = source_array(j, i) Next j Next i Else For i = 1 To numRows For j = 1 To numCols target_range.Cells(i, j).Value = source_array(i, j) Next j Next i End If PasteArray = 0 Exit Function ErrorHandler: PasteArray = -1 End Function
なるほど、一次元も二次元も、ともに二次元配列にしたうえで張り付けるのか。
ちなみに、以前作成した際に不便だった点は、文字列が配列に格納されると同時に数値に変換されてしまうことだった。追加で指示してみよう。
Function PasteArray(target_range As Range, source_array As Variant, Optional transpose_flag As Boolean = False) As Integer Dim i As Long, j As Long Dim numRows As Long, numCols As Long On Error GoTo ErrorHandler ' 配列が2次元または1次元であるかどうかを確認 If IsArray(source_array) = False Then PasteArray = -1 Exit Function End If ' 配列の次元数を取得 Select Case True Case IsArray(source_array) If Not (IsArray(source_array) And IsArray(source_array(1))) Then ' 1次元配列の場合 numRows = 1 numCols = UBound(source_array) - LBound(source_array) + 1 Else ' 2次元配列の場合 numRows = UBound(source_array, 1) - LBound(source_array, 1) + 1 numCols = UBound(source_array, 2) - LBound(source_array, 2) + 1 End If Case Else PasteArray = -2 Exit Function End Select ' 縦横を入れ替える場合 If transpose_flag Then For i = 1 To numCols For j = 1 To numRows target_range.Cells(i, j).Value = CStr(source_array(j, i)) Next j Next i Else For i = 1 To numRows For j = 1 To numCols target_range.Cells(i, j).Value = CStr(source_array(i, j)) Next j Next i End If PasteArray = 0 Exit Function ErrorHandler: PasteArray = -1 End Function
さらに、列の次元数を取得したうえで、縦横を入れ替えた配列を取得する部分を切り出して別の関数で作成してみよう。
'［用 途］ ' 指定セルに配列を貼り付ける。 '［引 数］ ' target_range As Range 配列を貼り付けるセル ' source_array As Variant 貼り付けられる配列 '［戻り値］ ' 0の場合 正常終了 ' -1の場合 異常終了 ※target_arrayは配列ではない。 ' -2の場合 異常終了 ※配列の次元数が３以上。
' 配列の次元数を取得する関数 Function GetArrayDimensions(arr As Variant) As Integer Dim dimCount As Integer dimCount = 0 On Error Resume Next Do dimCount = dimCount + 1 Loop Until IsEmpty(LBound(arr, dimCount)) On Error GoTo 0 GetArrayDimensions = dimCount - 1 End Function
' 配列の縦横を入れ替える関数 Function TransposeArray(arr As Variant) As Variant Dim numRows As Long numRows = UBound(arr, 1) Dim numCols As Long numCols = UBound(arr, 2) Dim result() As Variant ReDim result(1 To numCols, 1 To numRows) Dim i As Long Dim j As Long For i = 1 To numRows For j = 1 To numCols result(j, i) = arr(i, j) Next Next TransposeArray = result End Function
' 配列を指定したセル範囲に貼り付ける関数 Function PasteArray(target_range As Range, source_array As Variant, Optional transpose_flag As Boolean = False) As Integer On Error GoTo ErrorHandler ' 配列が有効であるかどうかを確認 If Not IsArray(source_array) Then PasteArray = -1 Exit Function End If ' 配列の次元数を取得 Dim arrayDimensions As Integer arrayDimensions = GetArrayDimensions(source_array) If arrayDimensions > 2 Then PasteArray = -2 Exit Function End If ' 配列の縦横を入れ替えるかどうかをチェック Dim transposedArray As Variant If transpose_flag Then If arrayDimensions = 1 Then ' 1次元配列の場合、単純に縦横を入れ替える Dim numRows As Long numRows = UBound(source_array) - LBound(source_array) + 1 Dim numCols As Long numCols = 1 ReDim transposedArray(1 To numRows, 1 To numCols) Dim i As Long For i = 1 To numRows transposedArray(i, 1) = source_array(i) Next i Else ' 2次元配列の場合、TransposeArray関数を使用 transposedArray = TransposeArray(source_array) numRows = UBound(transposedArray, 1) numCols = UBound(transposedArray, 2) End If Else transposedArray = source_array If arrayDimensions = 1 Then numRows = 1 numCols = UBound(source_array) - LBound(source_array) + 1 Else numRows = UBound(source_array, 1) numCols = UBound(source_array, 2) End If End If ' 値をセルに貼り付ける Dim j As Long For i = 1 To numRows For j = 1 To numCols target_range.Cells(i, j).Value = CStr(transposedArray(i, j)) Next Next PasteArray = 0 Exit Function ErrorHandler: PasteArray = -1 End Function
結果として、元々作成したものに似た形になってしまった。文字列として値を貼り付ける点が改善されたため、これも一つの進化系といえるかな。ＡＩさん、さすがです。
参考まで。
自作マクロ機能のAIアップグレード：FindAll
生成系ＡＩの出現により、ここ数年で色々なものが随分と様変わりした。
最近ではExcel VBAにおいても、仕様をAIに伝えて作ってもらうことが多くなった。
そこで今回は、以前作成したものの「いまいち」だったマクロを、改めてAIに添削してもらった。素材となるのはこちら。
infoment.hatenablog.com
添削結果がこちら。
Function FindAll(target_range As Range, _ faWhat As String, _ Optional faLookIn As Excel.XlFindLookIn = xlValues, _ Optional faLookAt As Excel.XlLookAt = xlPart, _ Optional faMatchCase As Boolean = False, _ Optional faMatchByte As Boolean = False) As Range Dim FindCell As Range Dim FirstAddress As String Dim TempRange As Range ' 最初の一致を見つける Set FindCell = target_range.Find(What:=faWhat, _ LookIn:=faLookIn, _ LookAt:=faLookAt, _ MatchCase:=faMatchCase, _ MatchByte:=faMatchByte) ' 一致するものがない場合、関数を終了する If FindCell Is Nothing Then Exit Function End If ' 最初に見つかったセルのアドレスを保存する FirstAddress = FindCell.Address Set TempRange = FindCell ' すべての一致を見つけるためにループ Do Set FindCell = target_range.FindNext(FindCell) If FindCell Is Nothing Then Exit Do ' セーフティチェック If FindCell.Address = FirstAddress Then Exit Do ' 新しいセルが既にTempRangeに含まれていないかを確認 If Intersect(TempRange, FindCell) Is Nothing Then Set TempRange = Union(TempRange, FindCell) End If Loop ' 一致するすべての範囲を返す Set FindAll = TempRange End Function
なるほど、確かにすっきりした。しかし、丸投げはよくない。テストしよう。
Sub test() FindAll(ActiveSheet.Cells, "ターゲット").Interior.Color = vbRed End Sub
結果がこちら。
AIさん、さすがです。
ご参考まで。
マインクラフト：メンガーのスポンジをコマンドで作成
最近、子供と一緒にマインクラフトで遊んでいる。
先日、メンガーのスポンジを作るコマンドを作ってみたので、備忘録がてら紹介。
ja.wikipedia.org
- X軸（よこ軸）
- Y軸（高さ軸）
- Z軸（たて軸）
とするとき、まず起点となるブロックを一つ置いてみる。
↓ ３×３×３の立方体の一段目。
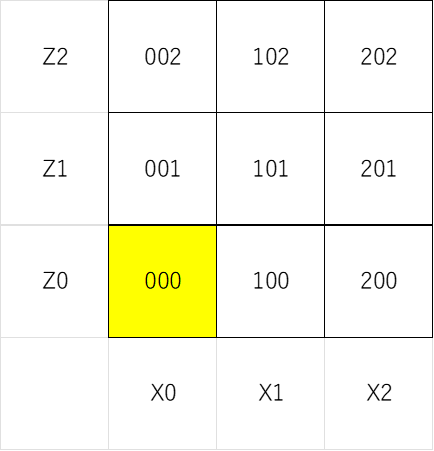
この000（相対座標）のブロックを、適切な箇所にコピーしていく。
白抜きの箇所が、コピーしてはいけない箇所。
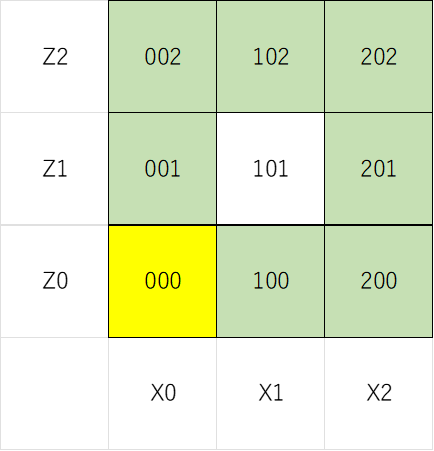
↓二段目（白抜きの箇所はコピー不可）。
↓三段目（白抜きの箇所はコピー不可）。
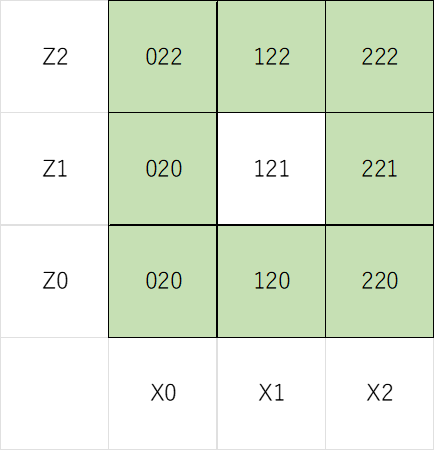
結果、このような基本形が出来上がる。
これを一つのブロックと見立てて、どうようにコピーを繰り返すことでフラクタル図形ができていく。
ところでこの「コピーする／しない」、何か法則を見つけて自動化できないか。
試しに表にしてみた。
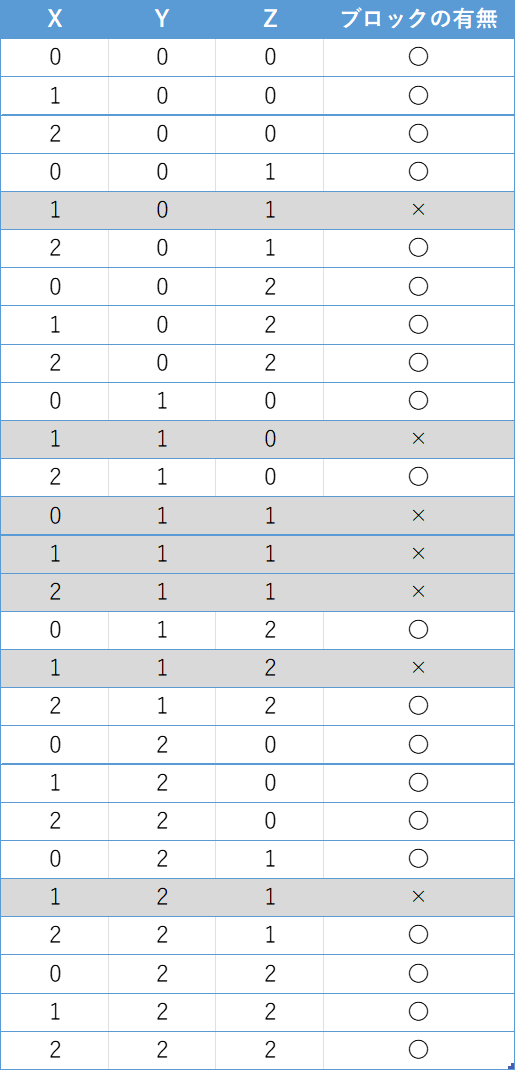
・・・法則が見つけられない。ということで、試しに全部１引いてみた。すると、０の数が２以上のときにコピー不可であることが分かった。
※恐らくは、すでに広く一般的に知られている法則と思われる。
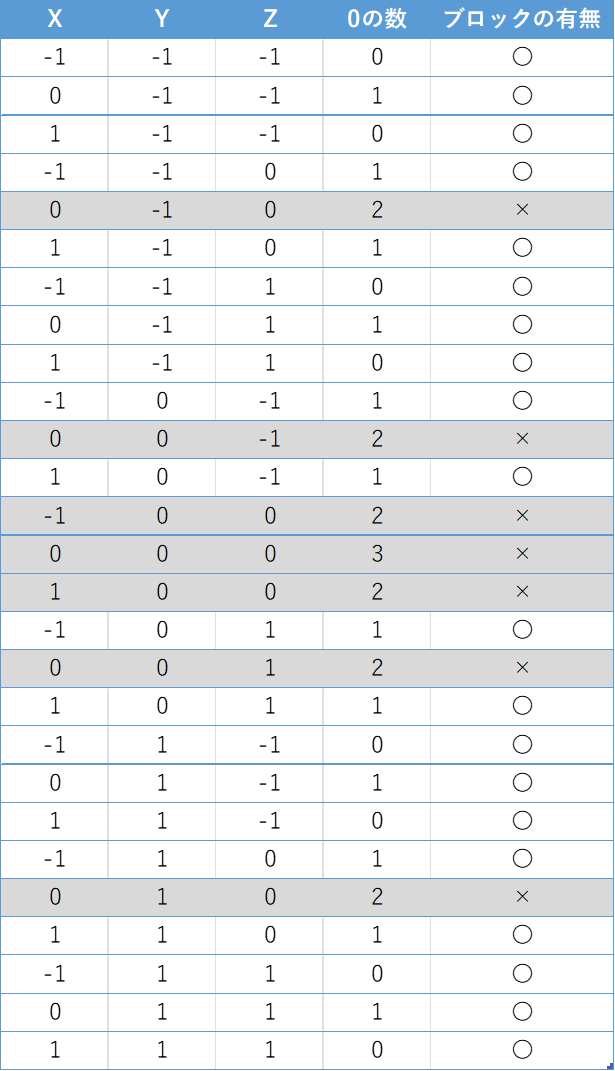
ここまでわかれば、あとはコマンド化するだけだ。というわけで作ってみた。
count_zeros = 0 def check_zeros(a: number, b: number, c: number): global count_zeros count_zeros = 0 if a == 0: count_zeros += 1 if b == 0: count_zeros += 1 if c == 0: count_zeros += 1 return count_zeros <= 1 def on_on_chat(origin_x, origin_y, origin_z): blocks.place(PLANKS_ACACIA, world(origin_x, origin_y, origin_z)) for n in range(5): for index_x in range(3): for index_y in range(3): for index_z in range(3): if check_zeros(index_x - 1, index_y - 1, index_z - 1): blocks.clone(world(origin_x, origin_y, origin_z), world(origin_x + 3 ** n - 1, origin_y + 3 ** n - 1, origin_z + 3 ** n - 1), world(origin_x + index_x * 3 ** n, origin_y + index_y * 3 ** n, origin_z + index_z * 3 ** n), CloneMask.REPLACE, CloneMode.NORMAL) player.on_chat("Menger_sponge", on_on_chat)
結果がこちら。
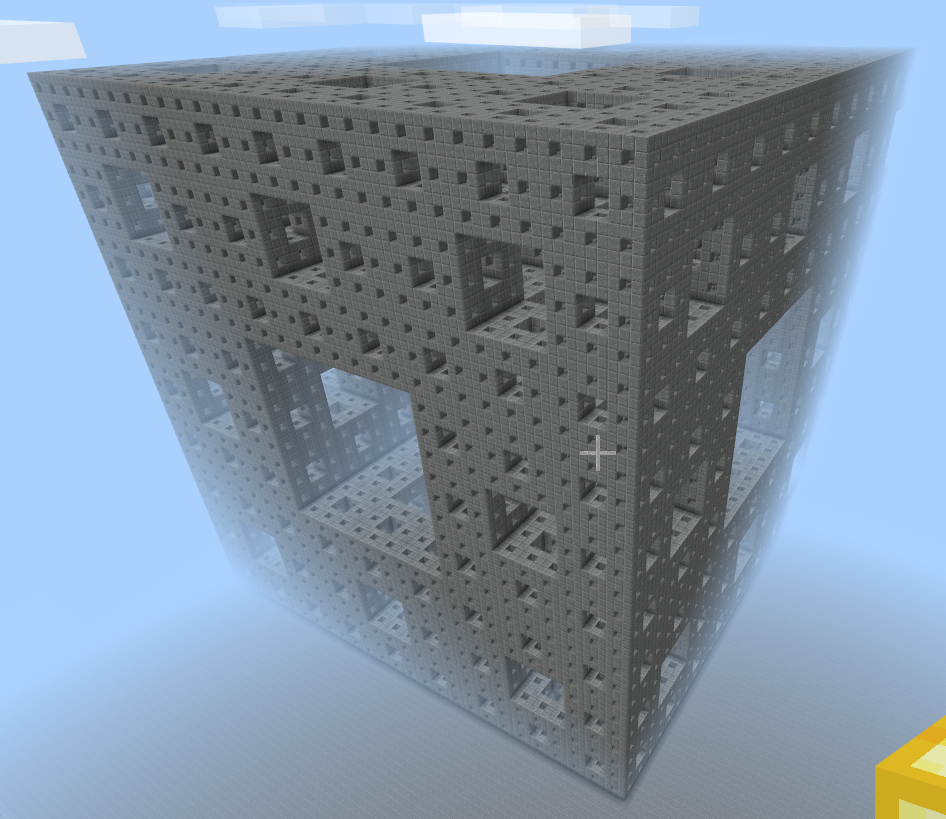
参考まで。
再びトーナメント表作成 ➈-6 特定名簿からの作成
特定名簿からのトーナメント作成ツールを、少しずつ紹介中。
本日も、昨日の続きから。
今日は、三つに分けたサブプロシージャの最後。
Dim Sh As Worksheet Set Sh = ActiveSheet ' トーナメント作成用シートを変数にセットしてリネーム。 Sh.Name = SheetName ' 各選手の「番号」を、辞書を利用して「人名」に置換。 For Each r In Sh.UsedRange.Columns(1).Cells If r <> vbNullString Then r = PDict(r.Value) End If Next ' 配列内で、選手名が空欄であれば「不戦敗」に置き換える。これにより、 ' 対戦相手がシード選手となる。 For i = 1 To UBound(arr) If arr(i, 列名.enNo) = vbNullString Then arr(i, 列名.enNo) = "不戦敗" ' 形のトーナメント作成である場合、この後に続く組手トーナメント作成時に ' 形と同カードが発生しないよう、形の対戦組み合わせを辞書に記録する。 ElseIf match_type = en形 Then If WorksheetFunction.IsOdd(i) Then If arr(i, 列名.enNo) <> vbNullString And arr(i + 1, 列名.enNo) <> vbNullString Then DDict(arr(i, 列名.enNo)) = arr(i + 1, 列名.enNo) DDict(arr(i + 1, 列名.enNo)) = arr(i, 列名.enNo) End If End If End If Next With DstTb If .ListRows.Count > 0 Then .DataBodyRange.Delete End If .ListRows.Add .DataBodyRange.Cells(1, 1).Resize(UBound(arr), UBound(arr, 2)) = arr End With If DuplicateTimes > 0 Then MsgBox SheetName & "で、二回戦までに " & DuplicateTimes & " 箇所で同所属選手対戦の恐れがあります。確認および調整をお願いします。" End If End Sub
これで、対戦表およびトーナメント作成までの機能が完成した。
それでは次回、実際に作成されたものをみてみよう。
参考まで。
※その後、数々の仕様変更があって、いったん保留となりました。
再びトーナメント表作成 ➈-5 特定名簿からの作成
特定名簿からのトーナメント作成ツールを、少しずつ紹介中。
本日も、昨日の続きから。
昨日は「前半と後半の二回に分ける」としたが、それでも長かった。
ということで、今日は中盤のご紹介。同一サブプロシージャの途中から始まるため分り難くなっているが、最後に改めてまとめて紹介するため、今はご勘弁。
Do With New VBAProject.Tournament ' トーナメント作成の初期設定。 ' 前回順位の最大値を取得し、それ以降をランダムに並び替える。 .init Tb.ListColumns(列名.enNo).DataBodyRange, True, _ WorksheetFunction.Max(Tb.ListColumns(列名.en前回形順位).DataBodyRange) + 1 ' トーナメントの配列取得。 arr = TournamentArray(.TournamentSortedOrderArray, match_type) ' 同所属対戦を不可とするブロック単位で、同所属の対戦が無いかを確認する。 For i = 1 To UBound(arr) Step DupTrial ' 重複の有無は辞書で行う。そのため、ループに入るたびに辞書を空にしている。 Dict.RemoveAll For j = 0 To DupTrial - 1 ' 一回戦においては空欄＝シードが存在するため、それ以外の場合で評価している。 ' keyの重複を不可とする仕様を利用しているため、itemは不問。今回はTrueとした。 If arr(i + j, 列名.en所属) <> vbNullString Then If Not Dict.Exists(arr(i + j, 列名.en所属)) Then Dict(arr(i + j, 列名.en所属)) = True Else ' 重複があった場合は、重複回数をカウントアップ。 DuplicateTimes = DuplicateTimes + 1 End If End If Next Next ' 重複回数が重複許容回数を下回る場合であって、且つ組手のトーナメントを作成している場合、 ' 一回戦で形トーナメントと同じ選手と対戦していないかを確認。対戦している場合は再組合せ。 If DuplicateTimes < AllowableDuplicateTimes And match_type = en組手 Then For i = 1 To UBound(arr) Step 2 If DDict.Exists(arr(i, 列名.enNo)) Then If DDict(arr(i, 列名.enNo)) = arr(i + 1, 列名.enNo) Then ' 同じ選手と対戦している場合、重複回数を強制的に重複許容回数とすることで ' 再抽選させる。 DuplicateTimes = AllowableDuplicateTimes Exit For End If End If Next End If ' ループ回数が最大値を超えた場合の処理。 If LoopCount > LoopCountMax Then MsgboxResult = MsgBox("組み合わせをランダムに" & LoopCountMax & "回作成しましたが、同所属の対戦を回避できませんでした。" & vbNewLine & _ "このままの組み合わせで継続しますか？", vbYesNo, "処理継続確認") If MsgboxResult = vbNo Then MsgBox "処理を中断しました。" Exit Sub Else ' 同所属の対戦があるままトーナメント作成。人の手で最終調整。 .CreateTournament Exit Do End If ' 重複回数が許容重複回数を下回っている場合、トーナメント作成の条件達成。 ' トーナメントを作成してループを抜ける。 ElseIf DuplicateTimes < AllowableDuplicateTimes Then .CreateTournament Exit Do End If End With LoopCount = LoopCount + 1 ' 重複回数の初期化。 DuplicateTimes = 0 Loop
以下の条件においては、どうしても一回戦での同一所属対戦が増えてしまう。
- 選手数が多く、且つ、参加団体数が少ない場合。
- 2^nよりもほんの少しだけ、参加人数が多い場合。
例えば2^4=16人より一人多い17人の場合について考えてみる。この場合、一回戦は１組のみで、残りの対戦はすべてシードとなる。
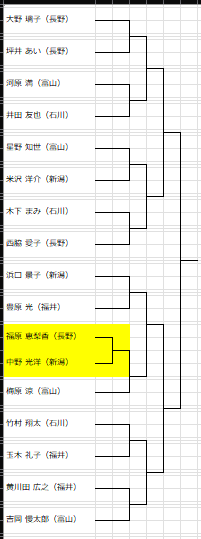
そのため、一回戦だけ同所属対戦を回避しても、どうしても二回戦（実質一回戦）での同一所属対戦が発生してしまう。
例）一回戦シードのため、二回戦で長野県同士で対戦となる。
これを回避すべく、昨日紹介範囲になるが、４人一組で同一部門の人がいないことを条件としてみた。
次回に続きます。
参考まで。
再びトーナメント表作成 ➈-4 特定名簿からの作成
特定名簿からのトーナメント作成ツールを、少しずつ紹介中。
本日も、先日の続きから。
本日は、トーナメントの作成部分。長いので、前半と後半で日を分けて紹介。
Sub 対戦表作成(Optional match_type As MatchType = en形) Call 名簿データ取得 ' 形および組手の名簿は、PowerQueryで作成。 ' 名簿テーブル。 Dim Tb As ListObject ' 対戦表テーブル。 Dim DstTb As ListObject ' トーナメントを作成するシート名。 Dim SheetName As String Select Case match_type Case MatchType.en形 Set Tb = S22_名簿_形.Tb Set DstTb = S24_対戦表_形.Tb Set DDict = New Scripting.Dictionary SheetName = "形トーナメント" Case MatchType.en組手 Set Tb = S23_名簿_組手.Tb Set DstTb = S25_対戦表_組手.Tb SheetName = "組手トーナメント" End Select ' 作成済みシートの有無確認。ある場合は削除する。 Dim Ws As Worksheet Application.DisplayAlerts = False For Each Ws In Worksheets If Ws.Name = SheetName Then Ws.Delete Exit For End If Next Application.DisplayAlerts = True ' 名簿テーブルの更新。BackgroundQueryをFalseにすることで、 ' QueryTableの更新が終わってから次のステップに進む。 Tb.QueryTable.Refresh BackgroundQuery:=False ' 組み合わせ表を格納するための配列。 Dim arr As Variant ' 同一所属間対戦をチェックするための辞書。 Dim Dict As Scripting.Dictionary Set Dict = New Scripting.Dictionary ' ループ用変数。 Dim i As Long Dim j As Long ' ループカウンタ。 Dim LoopCount As Long ' 重複数。形と組手で同じ人と対戦した回数。 Dim DuplicateTimes As Long ' 許容重複回数。 Dim AllowableDuplicateTimes As Long: AllowableDuplicateTimes = 2 ' 再履行許容回数。重複などが解消できない場合、無限ループに入る恐れがある。 ' そのため、再履行の最大値を設定しておく。 Dim LoopCountMax As Long: LoopCountMax = 10000 Dim MsgboxResult As VbMsgBoxResult Dim r As Range ' 同所属対戦を許容するブロックの人数。 ' 例）2 とした場合、一回戦のみ同所属対戦不可とする。 ' 4 とした場合、二回戦まで同所属対戦不可とする。一回戦がシードの場合、 ' 二回戦まで不可としておくことで、シード戦の同所属対戦を回避できる。 ' 出場団体が少ないほど同所属対戦が起きやすくなるため、調整が必要。 Dim DupTrial As Long: DupTrial = 4
以下の条件を如何に満足させるかが、今回苦労した点。
- 初戦での同門対決回避。
- 形と組手での同一組み合わせ回避。
結果、いくつかの辞書を作成しては中身を廃棄の繰り返しとなった。
きっと、もっとうまい方法があったに違いない。
次回に続きます。
参考まで。
再びトーナメント表作成 ➈-3 特定名簿からの作成
特定名簿からのトーナメント作成ツールを、少しずつ紹介中。
本日も、昨日の続きから。
昨日と同様の標準モジュールに、 以下を追加する。
' トーナメントの対戦順に並び替えられた配列に、その他の基本情報を付加して新たな配列を返す。 ' source_array：トーナメント対戦表。 ' match_type：形または組手の区分。 Function TournamentArray(source_array As Variant, match_type As MatchType) As Variant Dim i As Long ' データ格納用配列。 Dim arr() As Variant ReDim arr(1 To UBound(source_array), 1 To 列名.[_eLast] - 3) ' No.は、キー情報。通し番号または各団体の登録番号などを想定。 For i = 1 To UBound(source_array) arr(i, 1) = source_array(i) For Each p In Persons If source_array(i) = p.No Then arr(i, 列名.en名前) = p.名前 arr(i, 列名.enふりがな) = p.ふりがな arr(i, 列名.en性別) = p.性別 arr(i, 列名.en学校等区分) = p.学校等区分 arr(i, 列名.en学年) = p.学年 arr(i, 列名.en所属) = p.所属 Select Case match_type Case MatchType.en形 arr(i, 列名.en形出場) = p.形出場 arr(i, 列名.en前回形順位) = p.前回形順位 Case MatchType.en組手 arr(i, 列名.en形出場) = p.組手出場 arr(i, 列名.en前回形順位) = p.前回組手順位 End Select End If Next Next TournamentArray = arr End Function
少し短いが、しばらく毎日更新も目標の一つのため、今日はここまで。
参考まで。
