久しぶりの「三角関数の合成」 - Infomentのブログ～Excel VBA奮闘記～

先日、長男（高２）の数学で、久しぶりに「三角関数の合成」と再会した。
懐かしさのあまり、復習してみた。
$asinθ+bcosθ=\sqrt{a^2+b^2}sin(θ+α)$
ただし $角度α$ は、下図でいえばｘ軸と線分ACの成す角度とする。

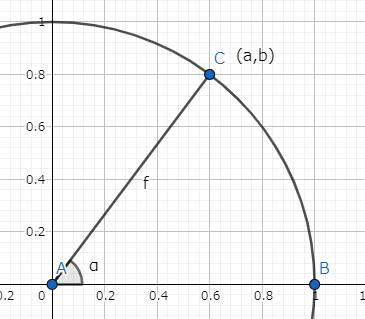
この円の半径 $ｒ$ は、三平方の定理から次のように求まる。
$r=\sqrt{a^2+b^2}$
また、三角比の定義によりａ，ｂはそれぞれ以下のとおり。
$a=rcosα$
$b=rsinα$
ゆえに最初の式に戻ると、加法定理により
$asinθ+bcosθ=r(sinθcosα+cosθsinα)=\sqrt{a^2+b^2}sin(θ+α)$
となる。

教科書ではその後に、このような練習問題が。
$\sqrt{3}sinθ+cosθ$
これは、
$cosα=\dfrac{a}{\sqrt{a^2+b^2}}=\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}^2+1^2}}=\dfrac{\sqrt{3}}{2}$
であるから、
$α=\dfrac{π}{6}$
となって、答えは
$2sin(θ+\dfrac{π}{6})$
となる。実際グラフを描いてみれば、両者はピッタリと一致する。